Circle Collisions
Hello I'm Phoenix Enero, and in this article (also my first) we will talk about Circular Collisions. But first, let me introduce myself.
I am a programmer in the Philippines. I originally programmed in a programming language called ActionScript 3.0, the programming language used in Flash, and made some pretty cool stuff with it, like a plotting program. After that, I stumbled on LÖVE through a ROBLOX (google it) group called "Love2D Fans". It was a great game engine, partly because it uses a simple programming language called Lua, and I made some games that I, erm, never finished. Okay, I think that's all I need to say about that. So anyways, let's get on with it!
And, before you comment here about that the code is not working, notice that I fixed most of my careless typos. If you have some problems, re-copy-and-paste the code.
Detecting Circular Collisions
First we need to find a way to detect circular collisions. The best way is to use distance checking. It checks if the distance between two circles' centers are less than the sum of their radii (plural of radius). The code will look like this.
function checkDistColl(circleA, circleB)
local dist = math.sqrt((circleA.x - circleB.x)^2 + (circleA.x - circleB.x)^2)
return dist <= circleA.radius + circleB.radius
end
However, if you want to optimize your code, you can square both sides, thus getting rid of the math.sqrt function on the left side, and squaring the sum of the radii on the right side.
function checkDistColl(circleA, circleB)
local dist = (circleA.x - circleB.x)^2 + (circleA.y - circleB.y)^2
return dist <= (circleA.radius + circleB.radius)^2
end
Collision Resolution
Now we want to know what will happen if they actually collide. But first, let's take a detour and find where the collisions occur.
Calculating the point of collision
This isn't really required for the collisions, but it can have some uses, for example, you can add an explosion effect at the point of the collision.
There are two ways to find the point, the right and the wrong way.
The wrong way, which many tutorials use, is averaging the two center points.
collPointX = (circleA.x + circleB.x)/2 collPointY = (circleA.y + circleB.y)/2
That works only if the circles have the same radius.
The right way that we want to use is a bit more complicated, but it works for circles of any radius:
collPointX ((circleA.x * circleB.radius) + (circleB.x * circleA.radius))/(circleA.radius + circleB.radius) collPointY ((circleA.y * circleB.radius) + (circleB.y * circleA.radius))/(circleA.radius + circleB.radius)
This gives the true x/y coordinates for the collision point. If you don't bother finding the collision point, try finding the midpoint of both circles, as it will be needed later on.
Bouncing Apart
Now, we know when our circles collide into each other, and we know their velocity and their x/y coordinates. How do we work out where they travel next?
There are two ways to do collisions; elastic collisions and inelastic collisions. Elastic collisions, in layman's terms, are collisions in which the objects do not "stick". Think billard balls colliding. Inelastic collisions are when they "stick". Think a bullet penetrating a block of wood. We will do elastic collisions here.
Explaining it in words can be difficult, so I'll add a gif image from Wikipedia. If you would like to learn, in detail, how the formula is derived, click the link in the caption of the image.

Usually, there are a lot of factors that influence collision, such as spin, mass, mass distribution, etc. but in this collision reaction, we will only use the mass factor. If you don't need that much realism, you can substitute mass for the radius of the circle.
The formula has something to do with the conservation of momentum. Momentum is expressed as this:
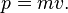
In words: momentum is mass times the velocity. The conservation of momentum says that, the sum of the momentum of 2 objects before the collision is equal to the sum of the momentum of the 2 objects after the collision. Assuming that the initial velocities are u, and the final velocities are v, the equation of the conservation of momentum is this:
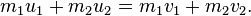
Now you have an equation with two unknowns, v1 and v2. To solve an equation with two unknowns, you need to find another equation with the same two unknowns in it. That happens to be dealing with kinetic energy. Kinetic energy is half of the mass times the magnitude of the velocity squared.

Now, it just so happens that, the sum of the kinetic energies of 2 objects before and after the collision remains the same. I have seen no equation-style image for that yet, so I'll just express it in code.
KE1 + KE3 = KE1Final + KE2Final
Expanding it, and factoring out the 1/2's in the kinetic energies (by multiplying both sides by 2) yelds:
(m1 * v1^2) + (m1 * v2^2) = (m1 * v1Final^2) + (m1 * v2Final^2)
Now you have a different equation with the same two unknowns. If you like algebra quite a bit, I invite you to sit down and try to solve both equations for both unknowns. In the mean time, I'll add Newton's Cradle here.

You done? The equations, solved for both unknowns, is this:

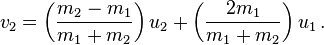
In code, that will look like this, after adding both fractions in each equation:
local newVelX1 = (circleA.vx * (circleA.mass - circleB.mass) + (2 * circleB.mass * circleB.vx)) / (circleA.mass + circleB.mass) local newVelY1 = (circleA.vy * (circleA.mass - circleB.mass) + (2 * circleB.mass * circleB.vy)) / (circleA.mass + circleB.mass) local newVelX2 = (circleB.vx * (circleB.mass - circleA.mass) + (2 * circleA.mass * circleA.vx)) / (circleA.mass + circleB.mass) local newVelY2 = (circleB.vy * (circleB.mass - circleA.mass) + (2 * circleA.mass * circleA.vy)) / (circleA.mass + circleB.mass)
But, if you have seen it, those values for newVelX1/Y1 and newVelX2/Y2, almost have the same fractions. Is there some way to optimize it? Yes there is. I won't explain the solution in detail, but basically, you find the total velocities of both objects. After getting the final velocity of objectA, you then add the total velocity and the final velocity of objectA to find the final velocity of objectB.
You can actually find the total velocity by subtracting both of the initial velocities. That may seem weird but think of it in the viewpoint of the system. Suppose you have a 40kph and 50 kph cars in a freeway, moving in the same direction. Depending on which car you are at, you can see one going at 10kph, or going at -10kph. In other words, it's either going away from you, or falling behind you.
So first, you find the total velocity before the collision. In code, for both axes, it will look like this:
local vxTotal = circleA.vx - circleB.vx local vyTotal = circleA.vy - circleB.vy
Then, you find the final velocity of circleA:
local newVelX1 = (circleA.vx * (circleA.mass - circleB.mass) + (2 * circleB.mass * circleB.vx)) / (circleA.mass + circleB.mass) local newVelY1 = (circleA.vy * (circleA.mass - circleB.mass) + (2 * circleB.mass * circleB.vy)) / (circleA.mass + circleB.mass)
Now, you find the final velocity of circleB, using the method I told earlier:
local newVelX2 = vxTotal + newVelX1 local newVelY2 = vyTotal + newVelY1
Well that's better than the double formula. You can actually make this more optimized by using the normal vector, but I won't cover it here.
So now, are we done yet? Hmm, not quite.
Earlier, we made some position updates to our circles and then we check for collisions. Because of that, there is a chance that the two overlap and the velocity is not enough to seperate the two. A solution to that is to do some more math.
Find the midpoint of the 2 circles (or the collision point, if both circles have the same radius). Now set the centers of the two circles to be radius R away from the midpoint, but along the "line of collision". The code will look like this:
midpointX = (circleA.x + circleB.x)/2 midpointY = (circleA.y + circleA.y)/2 dist = math.sqrt((circleA.x - circleB.x)^2 + (circleA.y - circleB.y)^2) circleA.x = midpointX + circleA.radius * (circleA.x - circleB.x)/dist circleA.y = midpointY + circleA.radius * (circleA.y - circleB.y)/dist circleB.x = midpointX + circleB.radius * (circleB.x - circleA.x)/dist circleB.y = midpointY + circleB.radius * (circleB.y - circleA.y)/dist
That (circleA.x - circleB.x)/dist there is a "normal" vector, that is, a vector with a direction, but with a magnitude of 1, and that is used here to move the circles along the line of collision.
Now, our complete code for the collision resolution function is this:
function circleResolution(circleA, circleB)
if checkCircleColl(circleA, circleB) then
-- Find the new velocities
local vxTotal = circleA.vx - circleB.vx
local vyTotal = circleA.vy - circleB.vy
local newVelX1 = (circleA.vx * (circleA.mass - circleB.mass) + (2 * circleB.mass * circleB.vx)) / (circleA.mass + circleB.mass)
local newVelY1 = (circleA.vy * (circleA.mass - circleB.mass) + (2 * circleB.mass * circleB.vy)) / (circleA.mass + circleB.mass)
local newVelX2 = vxTotal + newVelX1
local newVelY2 = vyTotal + newVelY1
-- Move the circles so that they don't overlap
local midpointX = (circleA.x + circleB.x)/2
local midpointY = (circleA.y + circleA.y)/2
local dist = math.sqrt((circleA.x - circleB.x)^2 + (circleA.y - circleB.y)^2)
circleA.x = midpointX + circleA.radius * (circleA.x - circleB.x)/dist
circleA.y = midpointY + circleA.radius * (circleA.y - circleB.y)/dist
circleB.x = midpointX + circleB.radius * (circleB.x - circleA.x)/dist
circleB.y = midpointY + circleB.radius * (circleB.y - circleA.y)/dist
-- Update the velocities
circleA.vx = newVelX1
circleA.vy = newVelY1
circleB.vx = newVelX2
circleB.vy = newVelY2
end
end
More than Two
That's good enough for two circles, but what about 3 or more? You need to use a double for-loop for that. The unoptimized way would be this:
for i=1, #objects do
local partA = objects[i]
for j=1, #objects do
local partB = objects[j]
if i ~= j then
-- check collision between partA and partB
end
end
end
I said that's unoptimized because, it checks for collisions that are already checked. Here's what it will look like for 4 objects.
object1 to object2, object3, object4 object2 to object1, object3, object4 object3 to object1, object2, object4 object4 to object1, object2, object3
If you look carefully, the first statement checks for collisions for object1 and object2. But in the next statement, you are checking for object2 and object1! Certainly, if object1 doesn't collide with the object2, then object2 is also not colliding to object1. A better, more optimized loop, will look like this:
for i=1, #objects-1 do
local partA = objects[i]
for j=i+1, #objects do
local partB = objects[j]
-- check collision between partA and partB
end
end
Now what the collision checking for 4 objects will look like this:
object1 to object2, object3, object4 object2 to object3, object4 object3 to object4 object4 to none
Object4 (or the last object in an object array) checks to none, because all of the others are checking for it. So you see that if you use the unoptimized way, it turns out that you checking the collisions 2 times as much.
Download the .love file (typos fixed by the way): circle-collision.love. As always, you can view the source code by either changing the extension to .zip and opening it, or opening it in an archive program like 7-zip.
And we are done!
Alright, now we are done with the collision resolution. I hope you learned something here, and if you have any questions or suggestions, please comment below!
Also, a credit goes to vrld for posting some suggestions too :).


Comments
josefnpat
Tue, 03/12/2013 - 04:12
Permalink
You've done a fantastic job, substitute541!
I really like your optimization technique for the Multiple Collision Detection section. I really need to implement this in my own programs!
Roland_Y
Wed, 03/13/2013 - 04:06
Permalink
substitute541
Wed, 03/13/2013 - 08:38
Permalink
Added a .love file. I also fixed lots of typos there too.
LuaWeaver
Thu, 03/14/2013 - 09:46
Permalink
Nice job! However, I think it should be added that the depth of the collision is math.max(radiusA,radiusB)-math.min(radiusA,radiusB) and that the depth might have an effect on the point of collision.
substitute541
Thu, 03/14/2013 - 21:37
Permalink
It does, but we are gonna move the 2 circles away from each other anyways. Also, what you said about the depth of the collision is exactly the same as math.abs(radA-radB). Think about it, the only difference between radA-radB and radB-radA is the signs of the number, not the number itself.
LoneArtisan
Thu, 01/09/2014 - 23:27
Permalink
A rectangle version of this would be helpful.
gingerbeardman
Wed, 12/02/2020 - 07:32
Permalink
Seems to be a typo?
midpointY = (circleA.y + circleA.y)/2
should be
midpointY = (circleA.y + circleB.y)/2
gingerbeardman
Wed, 12/02/2020 - 07:37
Permalink
here's a link to an archived copy of the .love file which indeed corrected the typo in my previous comment.
https://web.archive.org/web/20141220144830/https://dl.dropboxusercontent.com/u/105405645/Blog/LOVE2D%20Files/circle-collision.love